Reparametrization Tricks
Backpropagation of continuous and discrete random variables
Suppose we are interested in the marginal likelihood $\mathrm{p_{\theta}(x)}$. Consider a latent representation via variational autoencoder (VAE) (Kingma & Welling, 2013)
\[\begin{align} \mathrm{\log p_\theta(\mathbf{x})} &= \mathrm{\log \int p_\theta(\mathbf{x}, \mathbf{z}) \, d\mathbf{z}} \notag \\ &= \mathrm{\log \int q_\phi(\mathbf{z} \mid \mathbf{x}) \frac{p_\theta(\mathbf{x}, \mathbf{z})}{q_\phi(\mathbf{z} \mid \mathbf{x})} \, d\mathbf{z}} \notag \\ &\geq \mathrm{\mathbb{E}_{q_\phi(\mathbf{z} \mid \mathbf{x})} \log \frac{\overbrace{p_\theta(\mathbf{x}, \mathbf{z})}^{p_\theta(\mathbf{z}) p_\theta(\mathbf{x}\mid \mathbf{z})}}{q_\phi(\mathbf{z} \mid \mathbf{x})}} \notag \\ &=\mathrm{-D_{\mathrm{KL}}\left( q_\phi(\mathbf{z} \mid \mathbf{x}) \,\|\, p(\mathbf{z})\right)+\mathbb{E}_{q_\phi(\mathbf{z} \mid \mathbf{x})} \left[ \log p_\theta(\mathbf{x} \mid \mathbf{z}) \right]}, \notag \end{align}\]where $\geq$ follows from Jensen’s inequality, \(\mathrm{q_\phi(\mathbf{z} \mid \mathbf{x})}\) is the encoder, and \(\mathrm{p_\theta(\mathbf{x} \mid \mathbf{z})}\) is the decoder.
We denote the integrand by $\mathrm{f_\phi(\mathbf{z})}$ and write $\mathrm{q_\phi(\mathbf{z} \mid \mathbf{x})}$ simply as $\mathrm{q_\phi(\mathbf{z})}$. To optimize the loss function via backpropagation, the gradient of \(\mathrm{\mathbb{E}_{q_\phi(\mathbf{z})}[f_\phi(\mathbf{z})]}\) w.r.t. $\phi$ follows
\[\begin{align} \mathrm{\nabla_\phi \mathbb{E}_{q_\phi(\mathbf{z})}[f_\phi(\mathbf{z})] } &= \mathrm{\int_{\mathbf{z}} \nabla_\phi \left[ q_\phi(\mathbf{z}) f_\phi(\mathbf{z}) \right] \, d\mathbf{z} = \underbrace{\int_{\mathbf{z}} f_\phi(\mathbf{z}) \nabla_\phi q_\phi(\mathbf{z}) \, d\mathbf{z}}_{\text{Intractable if $q_\phi(\mathbf{z})\neq 0$}} + \mathbb{E}_{q_\phi(\mathbf{z})} \left[ \nabla_\phi f_\phi(\mathbf{z}) \right]}. \notag \end{align}\]We observe that the first term in RHS suffers from the large variance issue and is not differentiable.
Continuous Variables
Introducing a deterministic mapping $\mathrm{g_\phi:\mathbf{z} = g_\phi(\boldsymbol{\epsilon})}$, where $\boldsymbol{\epsilon} \sim q(\boldsymbol{\epsilon})$ (e.g. Gaussian) gives
\[\begin{align} \mathrm{\nabla_\phi \mathbb{E}_{q_\phi(\mathbf{z})}[f(\mathbf{z})] } &= \mathrm{\nabla_\phi \mathbb{E}_{q(\boldsymbol{\epsilon})}\left[ f\left(g_\phi(\boldsymbol{\epsilon})\right) \right] \approx \frac{1}{L} \sum_{l=1}^L \nabla_\phi f\left(g_\phi(\boldsymbol{\epsilon}^{(l)})\right)}, \notag \end{align}\]which is the well-known reparametrization trick in VAEs. For simplicity, the Gaussian distribution can be a multivariate Gaussian with a diagonal covariance structure.
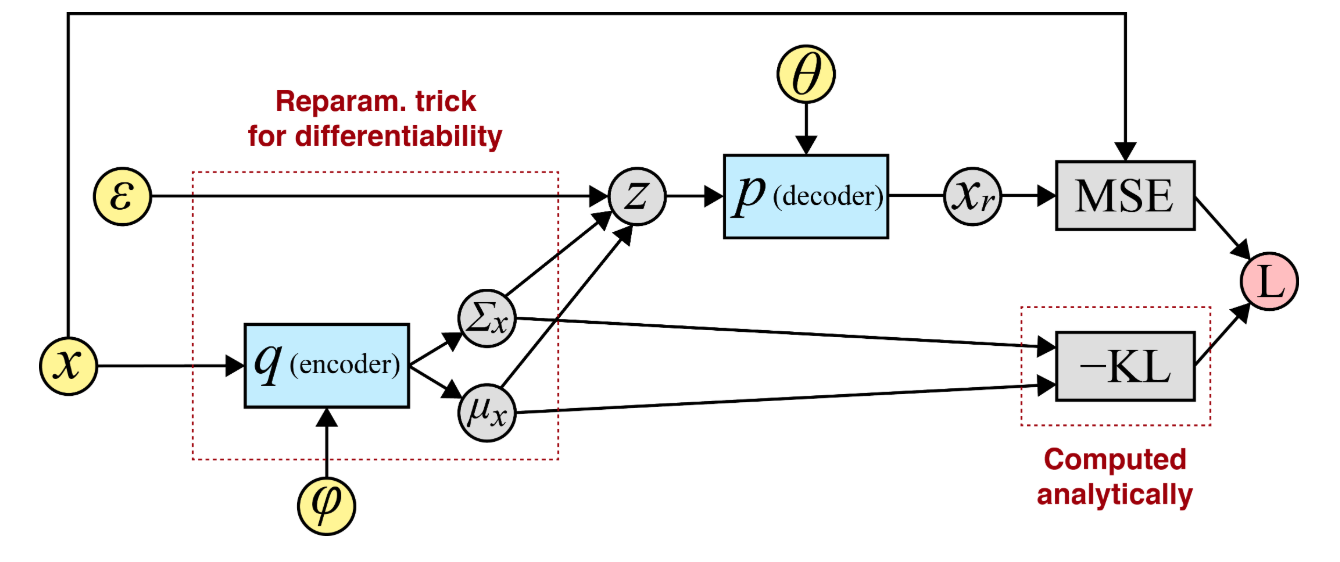
We further note that this one-step mapping from the data distribution to a Gaussian offers insight into the iterative transformations in diffusion models (Song et al., 2021).
Discrete Variables
When the latent variable $z$ in VAEs is a k-class categorical distribuion, the Gumbel-Max trick (Gumbel, 1954) proposes to draw samples $\mathbf{z}$ from a categorical distribution with k-class probabilities $\boldsymbol{\pi}$:
\[\begin{equation} \mathrm{\mathbf{z} = \mathrm{\text{one_hot}} \left( \arg\max_i \left[ g_i + \log \pi_i \right] \right)} \notag, \end{equation}\]where $\mathrm{g_1, \dots, g_k}$ are i.i.d. samples drawn from $\mathrm{Gumbel}(0, 1)$ link.
The Gumbel distribution is commonly used to model the distribution of the maximum (or minimum) of samples, with its CDF $\mathrm{F(x)=e^{-e^{-x}}}$. Invoking the inverse CDF trick, it is equivalent to drawing $\mathrm{-\log(-log(u_i))}$, where $\mathrm{u_i\sim Uniform(0, 1)}$.
To enable a differentiable approximation, (Jang et al., 2017) proposed a softmax relaxation s.t.
\[\begin{equation} \mathrm{\mathbf{z}_i \approx \frac{\exp\left((\log \pi_i + g_i)/\tau\right)}{\sum_{j=1}^k \exp\left((\log \pi_j + g_j)/\tau\right)}, \quad \text{for } i = 1, \dots, k .}\notag \end{equation}\]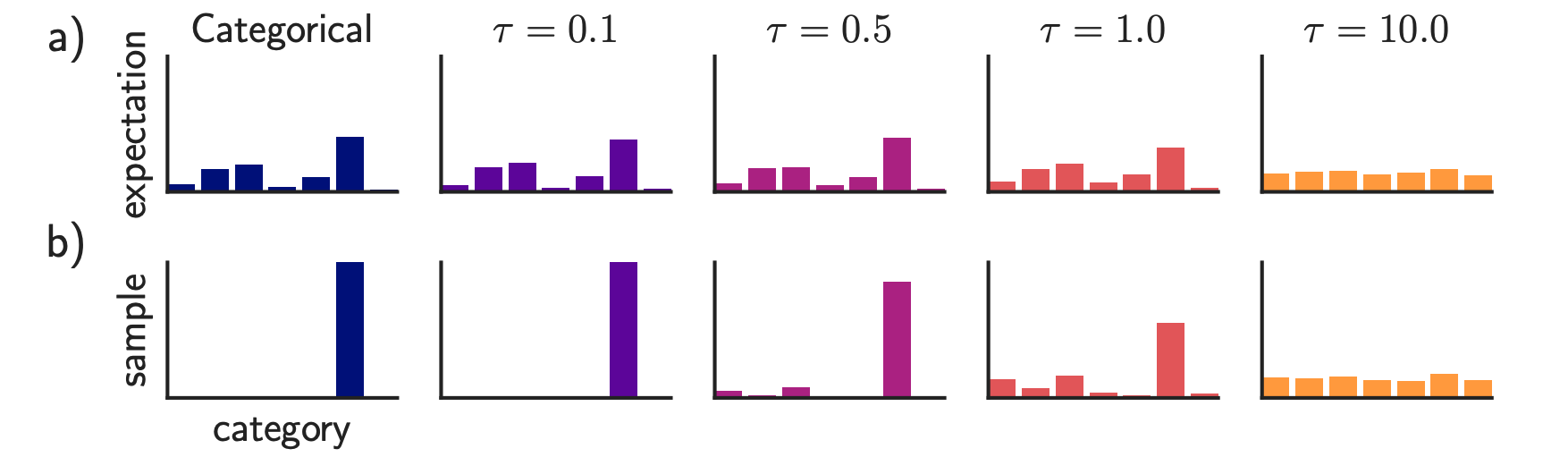
- Kingma, D. P., & Welling, M. (2013). Auto-Encoding Variational Bayes. ArXiv Preprint ArXiv:1312.6114.
- Song, Y., Sohl-Dickstein, J., P. Kingma, D., Kumar, A., Ermon, S., & Poole, B. (2021). Score-Based Generative Modeling through Stochastic Differential Equations. International Conference on Learning Representations (ICLR).
- Gumbel, E. J. (1954). Statistical theory of extreme values and some practical applications: a series of lectures (Number 33). US Govt. Print. Office.
- Jang, E., Gu, S., & Poole, B. (2017). Categorical Reparameterization with Gumbel-Softmax. Proceedings of the 5th International Conference on Learning Representations (ICLR).