Autoregressive Flow
The pioneering normalizing flows within generative models.
Normalizing Flows
Normalizing flows (Papamakarios et al., 2021) are the pioneers in generative models. The main idea is to transform a random vector $\mathrm{u}$ through an invertible transport map $\mathrm{T}$:
\[\begin{align} \mathrm{x}=\mathrm{T}(\mathrm{u}), \ \ \text{where}\ \mathrm{u}\sim \mathrm{p}_{\mathrm{u}}(\mathrm{u}).\notag \end{align}\]If $\mathrm{T}$ is bijective and differentiable, the density of $\mathrm{x}$ can be obtained by a change of variables
\[\begin{align} \mathrm{p}_{\mathrm{X}}(\mathrm{x})=\mathrm{p}_{\mathrm{u}}(\mathrm{u})\bigg|\text{det} \mathrm{J}_{\mathrm{T}}(\mathrm{u}) \bigg|^{-1}=\mathrm{p}_{\mathrm{u}}(\mathrm{T}^{-1}(\mathrm{X}))\bigg|\text{det} \mathrm{J}_{\mathrm{T}^{-1}}(\mathrm{u}) \bigg|.\notag \end{align}\]where \(\text{det}\ \mathrm{J}_{\mathrm{T}}(\mathrm{u})\) quantifies the change of volume w.r.t. u, such that \(\text{det}\ \mathrm{J}_{\mathrm{T}}(\mathrm{u}) \approx \frac{\text{Vol}(\mathrm{d} \mathrm{x})}{\text{Vol}(\mathrm{d} \mathrm{u})}\); the second equality holds since $\text{det} (\mathrm{A} \mathrm{A}^{-1})=1=\text{det} (\mathrm{A}) \text{det}(\mathrm{A}^{-1})$.
Composition Property
To model complex distributions, it is standard to conduct multiple transformations $\mathrm{T}_1$, $\mathrm{T}_2, \cdots$, $\mathrm{T}_K$ such that $\mathrm{T}=\mathrm{T}_K \circ \cdots \circ \mathrm{T}_2 \circ \mathrm{T}_1$. If \(\{\mathrm{T}_k\}_{k=1}^K\) are also bijective and invertible, we have
\[\begin{align} \mathrm{T}^{-1}&=(\mathrm{T}_K \circ \cdots \circ \mathrm{T}_2 \circ \mathrm{T}_1)^{-1}=\mathrm{T}_1^{-1} \circ \mathrm{T}_2^{-1} \circ \dots \mathrm{T}_K^{-1}.\label{iterative_maps} \\ \text{det} \ \mathrm{J}_{\mathrm{T}}(\mathrm{u})& = \text{det} \mathrm{J}_{\mathrm{T}_K \circ \dots \mathrm{T}_1}(\mathrm{u}) = \text{det} \mathrm{J}_{\mathrm{T}_1}(\mathrm{u}) \cdot \text{det} \mathrm{J}_{\mathrm{T}_2}(\mathrm{T}_1(\mathrm{u})) \cdot \text{det} \mathrm{J}_{\mathrm{T}_K}(\mathrm{T}_{K-1}(\cdots(\mathrm{T}_1(\mathrm{u})))).\notag \end{align}\]KL Divergence
Denote by $\phi$ and $\psi$ the parameters of $\mathrm{T}$ and $\mathrm{p}_{\mathrm{u}}(\mathrm{u})$, respectively. The forward KL divergence follows that
\[\begin{align} \mathrm{L}(\phi, \psi)&=\text{KL}(\mathrm{p}^{\star}_{\mathrm{X}}(\mathrm{x})\| \mathrm{p}_{\mathrm{X}}(\mathrm{x}; \phi, \psi)) \label{forward_KL} \\ &=-\mathbb{E}_{\mathrm{p}^{\star}_{\mathrm{X}}(\mathrm{x})} [\log \mathrm{p}_{\mathrm{X}}(\mathrm{x}; \phi, \psi)] + \text{const} \notag \\ &=-\mathbb{E}_{\mathrm{p}^{\star}_{\mathrm{X}}(\mathrm{x})} [\log \mathrm{p}_{\mathrm{u}}(\mathrm{T}^{-1}(\mathrm{x}; \phi); \psi) + \log |\text{det} \mathrm{J}_{\mathrm{T}^{-1}}(\mathrm{x}; \phi)|]+\text{const}. \notag \end{align}\]The forward KL divergence is well-suited to generate the data distribution if we can model the transport maps $\mathrm{T}$ efficiently as shown in the masked autoencoder below, but is less efficient in computing the model density $\mathrm{p}^{\star}_{\mathrm{X}}(\mathrm{x})$ due to the iterative maps in Eq.\eqref{iterative_maps}.
Alternatively, when we are interested to evaluate model density \(\mathrm{p}_{\mathrm{X}^{\star}}(\mathrm{x})\), we can try to optimize the reverse KL divergence
\[\begin{align} \mathrm{L}(\phi, \psi)&=\text{KL}(\mathrm{p}_\mathrm{X}(\mathrm{x}; \phi, \psi) \| \mathrm{p}^{\star}_{\mathrm{X}}(\mathrm{x})) \label{reverse_KL} \\ &=\mathbb{E}_{\mathrm{p}_{\mathrm{X}}(\mathrm{x}; \phi, \psi)} [\log \mathrm{p}_{\mathrm{X}}(\mathrm{x}; \phi, \psi) - \log \mathrm{p}_{\mathrm{X}}^{\star}(\mathrm{x})] \notag \\ &=-\mathbb{E}_{\mathrm{p}_{\mathrm{u}}(\mathrm{u}; \psi)} [\log \mathrm{p}_{\mathrm{u}}(\mathrm{u}; \psi) - \log |\text{det} \mathrm{J}_{\mathrm{T}}(\mathrm{u}; \phi)| - \log \mathrm{p}_{\mathrm{X}}^{\star}(\mathrm{T}(\mathrm{u}; \phi))]. \notag \end{align}\]In empirical training, we resrot to Monte Carlo samples to approximate the expectation.
Autogressive Flows
Autoregressive flows represent one of the earliest developments in flow-based models. We can map the data distribution $\mathrm{p}_\mathrm{X}(\mathrm{x})$ into a uniform distribution in $(0, 1)^\mathrm{D}$ using a transport map with a triangular Jacobian.
To achieve the goal of universal representation, we leverage conditional probability and decompose $\mathrm{p}_\mathrm{X}(\mathrm{x})$ into a product of conditional probabilities as follows
\[\begin{align} \mathrm{p}_{\mathrm{X}}(\mathrm{x}) = \Pi_{i=1}^\mathrm{D} \mathrm{p}_{\mathrm{X}}(\mathrm{x}_i | \mathrm{x}_{<i}).\label{seq_structure} \end{align}\]Define the transformation $\mathrm{F}$ to be the CDF function of the conditional density:
\[\begin{align} \mathrm{z}_i = \mathrm{F}_i(\mathrm{x}_i| \mathrm{x}_{<i})=\int_{-\infty}^{\mathrm{x}_i} \mathrm{p}_{\mathrm{X}}(\mathrm{x}_i'|\mathrm{x}_{<i}) \mathrm{d} \mathrm{x}_i'=\text{P}(\mathrm{x}_i'\leq \mathrm{x}_i | \mathrm{x}_{<i}).\notag \end{align}\]The invertibility of $\mathrm{F}$ leads to
\[\begin{align} \mathrm{x}_i = (\mathrm{F}_i(\cdot|\mathrm{x}_{<i}))^{-1} (\mathrm{z}_i) \text{ for } i=1,2,..., \mathrm{D}.\notag \end{align}\]Notably, the Jacobian of $\mathrm{F}$ is a lower trianagular matrix and the determinant of $\mathrm{F}$ is equal to the product of diagonal elemants.
\[\begin{align} \text{det} \mathrm{J}_\mathrm{F}(\mathrm{x}) = \Pi_{i=1}^\mathrm{D} \frac{\partial \mathrm{F}_i}{\partial \mathrm{x}_i} = \Pi_{i=1}^\mathrm{D} \mathrm{p}_\mathrm{X}(\mathrm{x}_i | \mathrm{x}_{<i})=\mathrm{p}_\mathrm{X}(\mathrm{x}).\notag \end{align}\]If there is another map $\mathrm{G}$ that transforms a general prior distribution to the uniform distribution $(0, 1)^\mathrm{D}$, the flow with transformation $\mathrm{T}=\mathrm{F}^{-1}\circ \mathrm{G}$ can map a general prior to the data distribution.
Modeling
Masked Autoencoder
To model the sequential structure \eqref{seq_structure} via an efficient parallelism, (Germain et al., 2015) abandoned the RNN encoder and proposed a mind-blowing idea by using an masked autoencoder. The code snippet is from (Karpathy, 2019).
class MaskedLinear(nn.Linear):
""" apply masks to a standard MLP """
def __init__(self, in_features, out_features, bias=True):
super().__init__(in_features, out_features, bias)
self.register_buffer('mask', torch.ones(out_features, in_features))
def set_mask(self, mask):
self.mask.data.copy_(torch.from_numpy(mask.astype(np.uint8).T))
def forward(self, input):
return F.linear(input, self.mask * self.weight, self.bias)
The challenge is to design proper masks to satisfy the autoregressive (triangular) property. A good tutorial is provided below (Khapra, 2019).
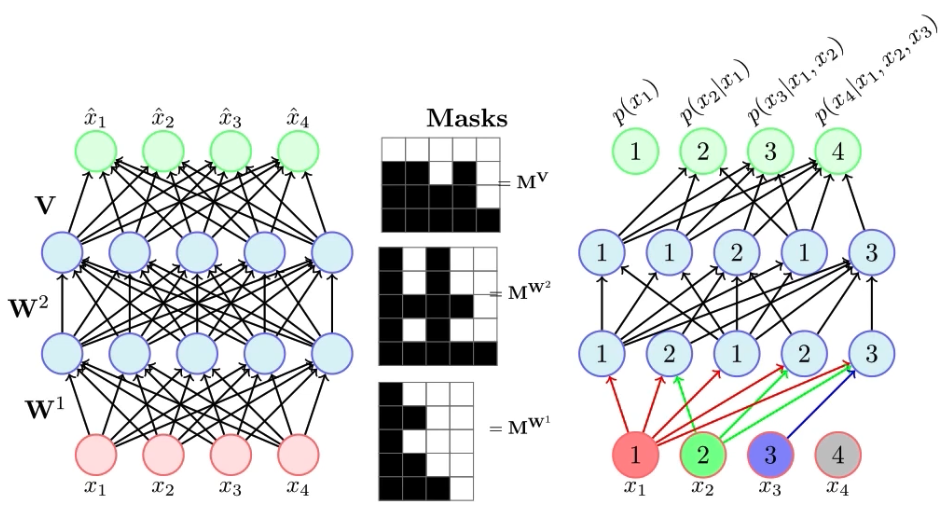
To ensure the output $\tilde x_d$ only depend on the preceding inputs $x_{<d}$.
- Assign the $k$-th hidden unit some random number $m(k)$ in $\{1, 2, \cdots, D-1\}$, which is the maximum number of input units that can be connected.
# sample the order of the inputs and the connectivity of all neurons
self.m[-1] = np.arange(self.nin) if self.natural_ordering else rng.permutation(self.nin)
for l in range(L):
self.m[l] = rng.randint(self.m[l-1].min(), self.nin-1, size=self.hidden_sizes[l])
- For any layers except the last one, the mask value is \(1_{m(k)\geq d}\) for the $d$-th output; The sign is changed to $>$ for the last layer.
# construct the mask matrices
masks = [self.m[l-1][:,None] <= self.m[l][None,:] for l in range(L)]
masks.append(self.m[L-1][:,None] < self.m[-1][None,:])
Masked Autogressive Flow (MAF)
MAF (Papamakarios et al., 2017) propose to optimize the reverse KL objective \eqref{reverse_KL}, which is efficient in the conditional density estimation while the sampling stage is slow in high dimensions because we need to iterate the dimension sequentially. To help understand the masked autoregressive flow, I simplified (Karpathy, 2019)’s code template and added some edits and comments.
from nflib.made import ARMLP
class MAF(nn.Module):
""" Masked Autoregressive Flow that uses a MADE-style network for fast forward """
def __init__(self, dim, parity, net_class=ARMLP, nh=24):
super().__init__()
self.dim = dim
self.net = net_class(dim, dim*2, nh)
self.parity = parity
def forward(self, x):
s, t = self.net(x)
z = x * torch.exp(s) + t
# permute elements for efficiency - pg5 https://arxiv.org/pdf/1705.07057.pdf
z = z.flip(dims=(1,)) if self.parity else z
log_det = torch.sum(s, dim=1)
return z, log_det
def backward(self, z):
x = torch.zeros_like(z)
log_det = 0
z = z.flip(dims=(1,)) if self.parity else z
for i in range(self.dim): # iterative sampling from d=1 to D
s, t = self.net(x.clone()) # clone to avoid in-place op errors if using IAF
x[:, i] = (z[:, i] - t[:, i]) * torch.exp(-s[:, i])
log_det += -s[:, i]
return x, log_det
class NormalizingFlowModel(nn.Module):
""" A Normalizing Flow Model is a (prior, flow) pair """
def __init__(self, prior, af_flows):
super().__init__()
self.prior = prior
self.af_flow = nn.ModuleList(af_flows)
def iterate(self, data, direction=1):
log_det = torch.zeros(data.shape[0])
for af_flow in self.af_flow[::direction]:
cur_flow = af_flow.forward if direction == 1 else af_flow.backward
data, ld = cur_flow(data)
log_det += ld
return data, log_det
def forward(self, x):
z, log_det = self.iterate(x, direction=+1)
prior_logprob = self.prior.log_prob(z).view(x.size(0), -1).sum(1)
return z, prior_logprob, log_det
def backward(self, z):
return self.iterate(z, direction=-1)
def sample(self, num_samples):
z = self.prior.sample((num_samples,))
x, _ = self.iterate(z, direction=-1)
return x
Inverse Autogressive Flow (IAF)
Similar to MAF, IAF (Kingma et al., 2016) proposed to flip the backward and forward sampling to speed up the sampling efficiency. The density estimation, however, becomes slower. The optimization corresponds to the forward KL divergence.
class IAF(MAF):
def __init__(self, *args, **kwargs):
super().__init__(*args, **kwargs)
self.forward, self.backward = self.backward, self.forward
- Papamakarios, G., Nalisnick, E., Rezende, D. J., Mohamed, S., & Lakshminarayanan, B. (2021). Normalizing Flows for Probabilistic Modeling and Inference. Journal of Machine Learning Research.
- Germain, M., Gregor, K., Murray, I., & Larochelle, H. (2015). MADE: Masked Autoencoder for Distribution Estimation. ICML.
- Karpathy, A. (2019). pytorch-normalizing-flows. Github: https://github.com/karpathy/pytorch-normalizing-flows
- Khapra, M. M. (2019). Masked Autoencoder Density Estimator (MADE). Deep Learning Part - II (CS7015): Lec 21.2. https://www.youtube.com/watch?v=lNW8T0W-xeE
- Papamakarios, G., Pavlakou, T., & Murray, I. (2017). Masked Autoregressive Flow for Density Estimation. NeurIPS.
- Kingma, D. P., Salimans, T., Jozefowicz, R., Chen, X., Sutskever, I., & Welling, M. (2016). Improved Variational Inference with Inverse Autoregressive Flow. NIPS.