Implicit Ridge Regularization
The optimal penalty can be zero or negative for real-world high dimensional data.
Ridge Regression with $n\gg d$: Bias-variance trade-off
We study the ordinary linear regression
\[\begin{align} \mathcal{L}=\|\mathrm{y}-\mathrm{X} {\beta}\|_2^2.\notag\\ \end{align}\]where $\mathrm{X}\in \mathbb{R}^{n\times d}$ and is full rank. The solution follows that $\widehat \beta=(\mathrm{X}^\intercal \mathrm{X})^{-1} \mathrm{X} \mathrm{y}$.
However, $(\mathrm{X}^\intercal \mathrm{X})^{-1}$ is often poorly conditioned, which leads to a large prediction variance. To solve this issue, a standard technique is to consider the Tikhonov regularization through a $l_2$ penalty.
\[\begin{align} \mathcal{L}_{\lambda}=\|\mathrm{y}-\mathrm{X} {\beta}\|_2^2 + \lambda \|\beta\|_2^2.\notag\\ \end{align}\]The solution is given as follows
\[\begin{align} \widehat \beta_{\lambda}=(\mathrm{X}^\intercal \mathrm{X} + \lambda \mathrm{I})^{-1} \mathrm{X} \mathrm{y} \label{ridge_solution}. \end{align}\]Increasing $\lambda$ leads to a larger bias but also yields a smaller prediction variance.
Ridge Regression with $d\gg n$: Minimum-norm estimator (Kobak et al., 2020)
Taking the limit $\lambda \rightarrow 0$ in Eq.\eqref{ridge_solution}, we have
\[\begin{align} \widehat \beta_{0} = \lim_{\lambda \rightarrow 0}\widehat \beta_{\lambda}= \lim_{\lambda \rightarrow 0} \mathrm{V}\left[\dfrac{\mathrm{S}}{\mathrm{S}^2 + \lambda} \right] \mathrm{U}^\intercal \mathrm{y}=\mathrm{V} \mathrm{S}^{-1}\mathrm{U}^\intercal \mathrm{y}=\mathrm{X}^{+}\mathrm{y}.\label{solution} \end{align}\]where $\mathrm{X}=\mathrm{U} \mathrm{S} \mathrm{V}^\intercal$ by SVD decomposition, $\mathrm{U}$ and $\mathrm{V}$ are two orthogonal matrices. $\mathrm{X}^{+}=\mathrm{X}^\intercal (\mathrm{X} \mathrm{X}^\intercal)^{-1}$ is the pseudo-inverse of $\mathrm{X}$ (invertible since $\mathrm{X}$ is full rank).
We can easily verify that $\widehat \beta_{0}$ is a solution of $\mathrm{y}-\mathrm{X} {\beta}=0$ because
\[\begin{align} \|\mathrm{y}-\mathrm{X} \widehat{\beta}_0 \|_2 = \| \mathrm{y}-\mathrm{X} \mathrm{X}^{+}\mathrm{y} \|_2=\| \mathrm{y}-\mathrm{y} \|_2=0.\notag \end{align}\]Moreover, $\widehat \beta_{0}$ is the minimum-norm estimator in $l_2$
\[\begin{align} \widehat \beta_{0} = \text{argmin}_{\beta} \big\{\|\beta\|_2^2 \ \ \big| \ \big\| \mathrm{y}-\mathrm{X} \beta \|_2^2=0 \big\}. \notag \end{align}\]Proof:
For any $\beta$ that solves $\mathrm{y}-\mathrm{X} {\beta}=0$, we have $\mathrm{X} \big(\widehat \beta_{0} - \beta \big) = 0.$
Next, we proceed to show $(\widehat \beta_{0} - {\beta})\perp \widehat \beta_{0}$. By Eq.\eqref{solution}, we have
\[\begin{align} \big(\widehat \beta_{0} - {\beta} \big)^{\intercal} \widehat \beta_{0} = \big(\widehat \beta_{0} - {\beta} \big)^{\intercal} \mathrm{X}^\intercal (\mathrm{X} \mathrm{X}^\intercal)^{-1}\mathrm{y} = \big(\mathrm{X}\big(\widehat \beta_{0} - {\beta} \big)\big)^{\intercal} (\mathrm{X} \mathrm{X}^\intercal)^{-1}\mathrm{y}=0.\notag \end{align}\]This implies that
\[\begin{align} \| \beta \|_2^2 = \|\beta - \widehat\beta_0 + \widehat \beta_0\|_2^2 = \|\beta - \widehat\beta_0\|_2^2 + \|\widehat \beta_0\|_2^2\geq \|\widehat \beta_0\|_2^2.\notag \end{align}\]This result aligns with Occam’s Zazor, suggesting the simplest solution among all the possible alternatives.
Tuning of $\lambda$
We study the derivative of the risk function (Kobak et al., 2020)
\[\begin{align} \mathrm{R}(\widehat \beta_{\lambda})=\mathrm{E}\big[((\mathrm{x}^\intercal\beta+\epsilon) - \mathrm{x}^\intercal \widehat\beta_{\lambda})^2 \big]=(\widehat\beta_{\lambda}-\beta)^\intercal \Sigma (\widehat\beta_{\lambda}-\beta)+\sigma^2.\notag \end{align}\]We show that the optimal penalty can be $\lambda_{\text{opt}}\leq 0$ by showing $\frac{\partial \mathrm{R}(\widehat \beta_{\lambda})}{\partial \lambda} \bigg|_{\lambda=0} \leq 0$.
\[\begin{align} \frac{\partial \mathrm{R}(\widehat \beta_{\lambda})}{\partial \lambda}=2(\widehat\beta_{\lambda}-\beta)^\intercal \Sigma \frac{\partial \widehat \beta_{\lambda}}{\partial \lambda}.\notag \end{align}\]Plugging in the solution \eqref{solution}, we have
\[\begin{align} \frac{\partial \mathrm{R}(\widehat \beta_{\lambda})}{\partial \lambda}=2\beta^{\intercal}\Sigma (\mathrm{X}^{\intercal} \mathrm{X})^{+2}\mathrm{X}^\intercal \mathrm{y} - 2\mathrm{y}^\intercal \mathrm{X} (\mathrm{X}^\intercal \mathrm{X})^{+} \Sigma (\mathrm{X}^\intercal \mathrm{X})^{+2} \mathrm{X}^{\intercal} \mathrm{y}\label{relation}, \end{align}\]where $(\mathrm{X}^{\intercal} \mathrm{X})^{+n}=\mathrm{U} \mathrm{S}^{-n} \mathrm{V}^\intercal$. Applying Eq.\eqref{relation} to the spiked covariance model (Kobak et al., 2020), we find that $\frac{\partial \mathrm{E}[\mathrm{R}(\widehat \beta_{\lambda})]}{\partial \lambda} \bigg|_{\lambda=0} \leq 0$ under some conditions.
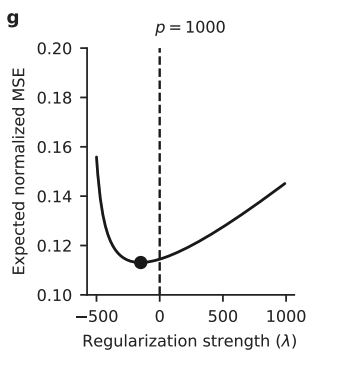
Extension to deep neural networks
Why does deep neural networks generalize so well? The following figure [credit to Belkin] tells us minimizing the smoothness might be the key.
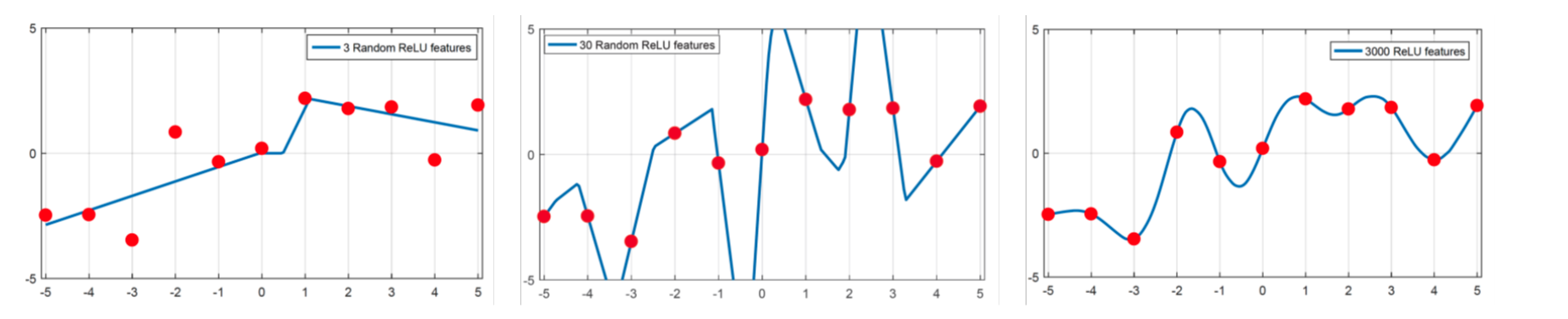
For the details, we refer interested readers to the study in (Belkin, 2021).
- Kobak, D., Lomond, J., & Sanchez, B. (2020). Optimal Ridge Penalty for Real-world High-dimensional Data can be Zero or Negative due to the Implicit Ridge Regularization. Journal of Machine Learning Research.
- Belkin, M. (2021). Fit Without Fear: Remarkable Mathematical Phenomena of Deep Learning through the Prism of Interpolation. Acta Numerica.