Inside the Transformers
Understanding the model architecture behind LLMs
Transformers are the building blocks of modern large language and visions models and have transformed the way we work and create. At their core is the attention mechanism (Vaswani et al., 2017), which captures complex temporal patterns and enables reasoning across sequences.
Softmax Attention
Attention computes weighted combinations of input tokens so that the model can focus on the most relevant parts of the sequence when producing each output.
\[\begin{align} \mathrm{\text{Attention}(Q, K, V)=\underbrace{\text{Softmax}\bigg(\frac{Q K^{\intercal}}{\sqrt{d}}\bigg)}_{\text{Attention weight} \ P} V} \notag \end{align}\]where $\mathrm{Q\in \mathbb{R}^{n\times d}}$, $\mathrm{K\in \mathbb{R}^{m\times d}}$, $\mathrm{V\in \mathbb{R}^{m\times d}}$, $\mathrm{d}$ is the hidden size. $n$ is the number of query positions and $m$ is number of KV positions. A scaling factor of $\frac{1}{\sqrt{d}}$ is employed to account for the linear variance.
In a self-attention example: “The VC will not invest money to the startup” with $\mathrm{n=m=L}$, an attention head may focus on the financial relation between VC and money, the syntactic dependency between VC and invest, or other types of relationships. Because the inner product is linear and softmax overly focuses on extreme values, we can only capture a single type of relationship.
Masks
Attention masks control what tokens can “see.” A bidirectional mask (no mask) lets tokens attend to all others (BERT (Devlin et al., 2019)), while a causal mask enforces left-to-right attention for generation (GPT). A padding mask ignores [PAD] tokens in batching, and an MLM mask randomly hides tokens (BERT’s [MASK]) for prediction from context.

def scaled_dot_product(q, k, v, mask=None):
d = q.size(-1)
scores = (q @ k.transpose(-2, -1)) / d**0.5
if mask is not None:
scores = scores.masked_fill(mask, float('-inf'))
attn = torch.softmax(scores, dim=-1)
return attn @ v, attn
Multi-head Attention (MHA)
To integrate knowledge from different representation subspaces, multi-head attention proposes an ensemble of locally linear projections of queries, keys and values
\[\begin{align} \mathrm{\text{MHA}(X_Q, X_K, X_V)} &= \mathrm{[\text{Head}_1; \text{Head}_2; \ldots, \text{Head}_h] W^O} \notag \\ \mathrm{\text{Head}_i} &= \mathrm{\text{Attention}(X_Q W_i^Q, X_K W_i^K, X_V W_i^V)}, \notag \end{align}\]where $\mathrm{W_i^Q, W_i^K , W_i^V \in \mathbb{R}^{d\times d_{\text{embed}}/h}}$ and $\mathrm{W^O \in \mathbb{R}^{d_{\text{embed}}\times d}}$ are the model parameters. Increasing the number of heads $\mathrm{h}$ enhances representational diversity, but also introduces a low-rank bottleneck within each head (Bhojanapalli et al., 2020). The model architecture is listed below:
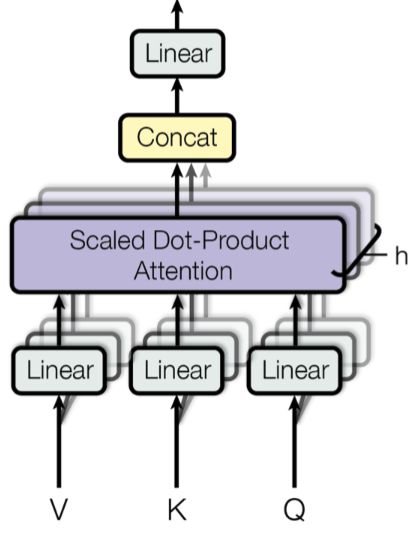
class MultiHeadAttention(nn.Module):
def __init__(self, input_dim, embed_dim, num_heads, bias=True):
super().__init__()
assert embed_dim % num_heads == 0, "embed_dim must be divisible by num_heads"
self.embed_dim = embed_dim
self.num_heads = num_heads
self.head_dim = embed_dim // num_heads
self.qkv_proj = nn.Linear(input_dim, 3 * embed_dim, bias=bias)
self.o_proj = nn.Linear(embed_dim, input_dim, bias=bias)
def forward(self, x, mask=None):
B, L, _ = x.size()
qkv = self.qkv_proj(x) # (B,L,3*E)
qkv = qkv.view(B, L, self.num_heads, 3*self.head_dim).permute(0, 2, 1, 3)
q, k, v = qkv.chunk(3, dim=-1) # each (B,H,L,D)
values, attention = scaled_dot_product(q, k, v, mask=mask)
values = values.permute(0, 2, 1, 3).reshape(B, L, self.embed_dim)
out = self.o_proj(values)
return out, attention
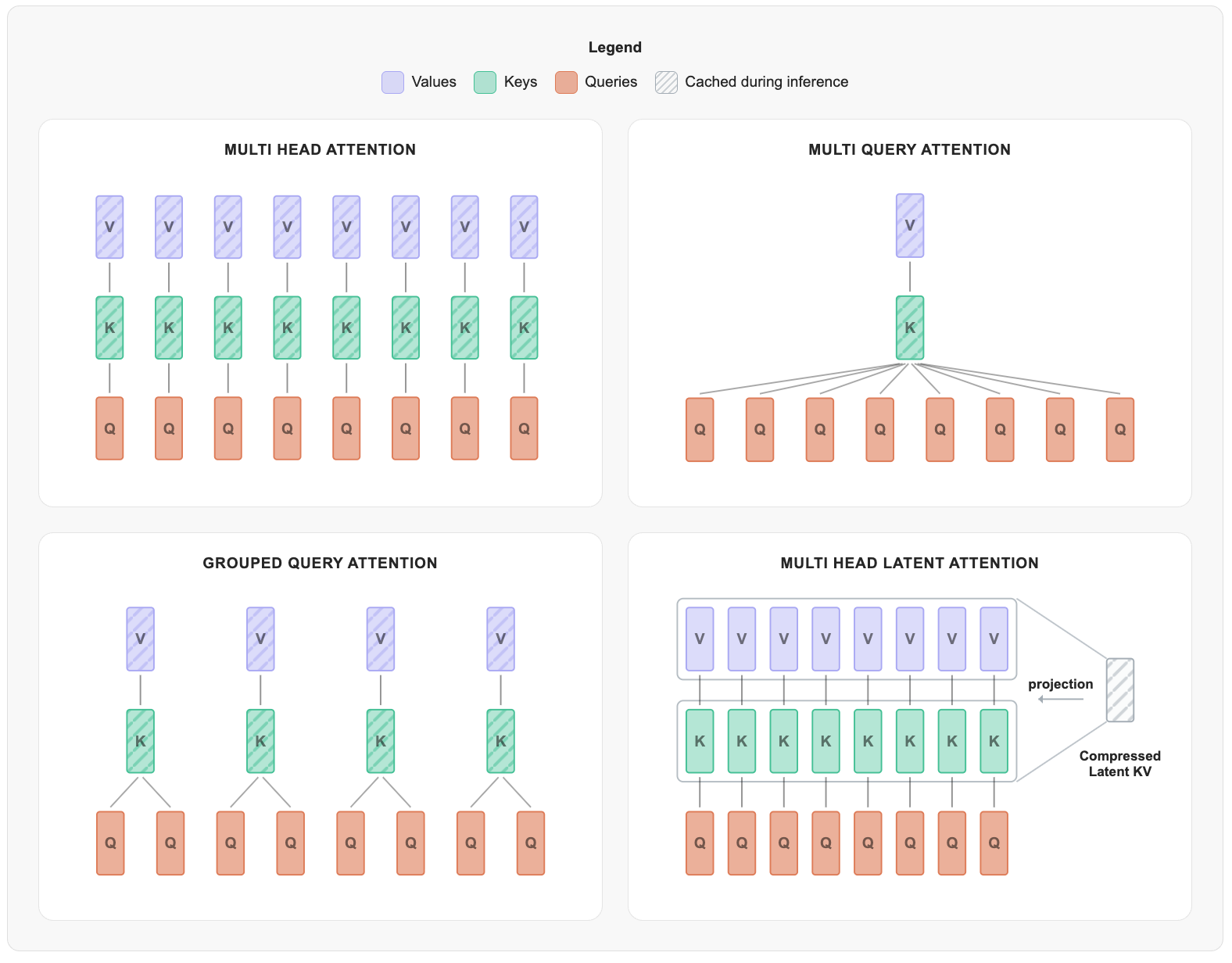
KV Cache in Inference
Let $\mathrm{x_{1:t}=(x_1, x_2, …, x_t)}$ denote the token sequence up to step $\mathrm{t}$. Each transformer layer computes the query/ key/ value vectors $\mathrm{q_i=x_i W^Q, k_i=x_i W^K, v_i=x_i W^V}$ for $\mathrm{i\in\{1, …, t\}}$. In the inference of autoregressive transformers, the attention output at position $\mathrm{t}$ is
\[\begin{align} \mathrm{H_t= \text{Softmax}\bigg(\frac{q_t K_{1:t}^{\intercal}}{\sqrt{d}}\bigg) V_{1:t}}, \notag \\ \mathrm{K_{1:t}} = \begin{bmatrix} \mathrm{k_1} \\ \vdots \\ \mathrm{k_t} \end{bmatrix}, \quad \mathrm{V_{1:t}} = \begin{bmatrix} \mathrm{v_1} \\ \vdots \\ \mathrm{v_t} \end{bmatrix}.\notag \end{align}\]To avoid the quadratic cost of repeatly computing all key value vectors $\mathrm{k_{1:t}}$ and $\mathrm{v_{1:t}}$ at each timestamp $\mathrm{t}$. We only need to compute the key-value pair $\mathrm{k_t, v_t}$ and update the cache as follows
\[\begin{align} \mathrm{K_{1:t}} = \begin{bmatrix} \mathrm{K_{1:t-1}} \\ \mathrm{k_t} \end{bmatrix}, \quad \mathrm{V_{1:t}} = \begin{bmatrix} \mathrm{V_{1:t-1}} \\ \mathrm{v_t} \end{bmatrix}.\notag \end{align}\]Beyond MHA
To lower KV cost with minimal quality loss, grouped query attention (GQA) shares keys and values across groups of attention heads, while multi-head Latent Attention (MLA) (Authors, 2024) compresses the keys and values into a latent vector. Experiments in (Allal et al., 2025) show that this can reduce KV usage by roughly 75% without hurting performance.
Efficient Attentions
Self-attention requires $\mathrm{O(L^2)}$ time and memory complexity for the length-$\mathrm{L}$ sequence generation. To mitigate the cost, one can exploit structural properties of the attention weight $\mathrm{P}$, such as linear attention (Katharopoulos et al., 2020), sliding window attention (SWA) (Jiang & Team, 2023), sparsity (Child et al., 2019) (Beltagy et al., 2020), low-rankness (Wang et al., 2020), and Kernelization (Choromanski et al., 2021), among others (Tay et al., 2022):
- 1. Linear Attention (Autoregressive Transformers v.s. RNNs): Consider a linear relaxation of the exponential linear product (Katharopoulos et al., 2020):
Exploit the recurrency property and ignore the normalizing constant (Wang et al., 2025):
\[\begin{equation} \mathrm{S_t = S_{t-1} + v_t k_t^\top, \quad y_t = S_t q_t = \sum_{i=1}^t v_i k_i^\intercal q_t,} \notag \end{equation}\]where the key–value rank-1 pair $\mathrm{v_t k_t^\top}$ is written into the memory. Although the recurrent update lacks parallelism, this can be mitigated through chunkwise parallelism. One can further increase the expressiveness by replacing the linear inner product $\mathrm{k^\top q}$ with a feature map $\mathrm{\phi(k)^\top \phi(q)}$:
\[\begin{equation} \mathrm{S_t = S_{t-1} + v_t \phi(k_t)^\top ,\quad y_t = S_t \phi(q_t), }\notag \end{equation}\]where the choices of $\phi$ include $1+\mathrm{ELU}$ (Katharopoulos et al., 2020), random features (Choromanski et al., 2021), cosine functions, polynomial expansions, deterministic projections, among others.
Gated Linear Attention: Compressing all past pairs equally tends to degrade performance as sequence length grows. To solve this issue, a forgetting gate $\mathrm{G_t\in (0,1)^{d\times d}}$ proposes to learn a $\mathrm{x_t}$-dependent decaying matrix and may result in more hardware-efficient training:
\[\begin{equation} \mathrm{S_t = G_t \odot S_{t-1} + v_t k_t^\top , \qquad y_t = S_t q_t .}\notag \end{equation}\]
-
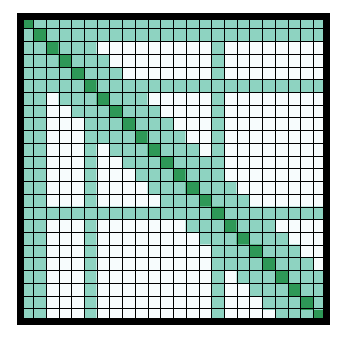
2. Sliding Window Attention Each token only attends to a local window of nearby tokens instead of the full sequence (Jiang & Team, 2023) to preverse local context information and scale to long sequences.
-
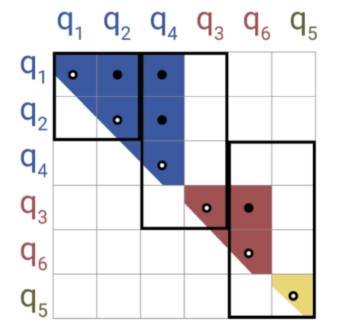
3. Sparse Attention: Longformer (Beltagy et al., 2020) leverages a (dilated) sliding window to capture local dependencies and assigns global attention to pre-specified tokens, enhancing modeling flexibility with $O(L)$ complexity. Reformer (Kitaev et al., 2020) employs Locality-Sensitive Hashing (LSH) to group similar items into the same buckets, and each query attends only to tokens within its bucket, resulting $O(L\log L)$ complexity.
-
4. Low-rank Attention: The query-key inner product acts as a rank-1 approximation to captur one similarity pattern. Although softmax relaxes this rank-1 constraint, the attention weight $\mathrm{P}$ remain approximately low-rank in practice (see Theorem 1 in (Wang et al., 2020)), yielding $O(L)$ complexity.
- 5. Kernelized Attention: The attention weight $\mathrm{P}$ can be viewed as an exponential kernel \(\mathrm{\exp(x^\intercal y)=\exp(\|x\|_2^2)K_{\text{gaussian}}(x, y) \exp(\|y\|_2^2)}\) and a prior random feature blog has ever discussed about the Monte Carlo approximations (Rahimi & Recht, 2007). Building on this idea, Performer (Choromanski et al., 2021) introduces non-negativity random features to avoiding singularities during normalization.
Position Embeddings
Absolute Positional Embedding
-
Learnable: A common approach is to use nn.Embedding for positional encodings, as in BERT (Devlin et al., 2019) and GPT-2, which is effective but limited by the training sequence length.
-
Sinusoidal: (Vaswani et al., 2017) proposes a deterministic, non-trainable encoding and is in spirit similar to random features (Rahimi & Recht, 2007).
Relative Position Encodings (RPE)
RPE augments the attention logits with terms that depend on $\mathrm{i-j}$ (Shaw et al., 2018; Dai et al., 2019):
\[\begin{equation} \mathrm{e_{ij}=\frac{Q_i^\top K_j}{\sqrt{d}} + Func(i-j, Q_i, K_j)}.\notag \end{equation}\]Attention with Linear Biases (ALiBi)
To achieve longer extrapolation length beyond the training length, (Press et al., 2022) penalizes distant key-value pairs
\[\begin{equation} \mathrm{e_{ij} = \frac{Q_i^\top K_j}{\sqrt{d}} + m_h (i - j)}, \notag \end{equation}\]where $\mathrm{m_h}$ is a fixed slope constant, e.g. $\mathrm{m_h=-\frac{1}{2^{h/H}}, h\in \{1, 2, …\}}$.
Rotary Position Embeddings (RoPE)
Building on insights from complex analysis, (Su et al., 2021) proposed a point-wise rotation of the Q/K matrices, which has since been widely adopted in state-of-the-art LLM architectures.
\[\begin{equation} \mathrm{e_{ij}=\frac{(R_i Q_i)^\top R_j K_j}{\sqrt{d}}=\frac{ Q_i\top R_{j-i} K_j}{\sqrt{d}}}.\notag \end{equation}\]where $\mathrm{R(\alpha)^\top R(\beta)=R(\beta-\alpha)}$ is the complex inner product and $\mathrm{R(\alpha)}$ is defined below
\[\begin{align} & \mathrm{z' = e^{im\theta} z =(\underbrace{\cos(m\theta) + i \sin(m\theta)}_{e^{im\theta}})(\underbrace{q_0 + i q_1}_{z})=} \underbrace{\begin{bmatrix} \mathrm{\cos(m\theta)} & -\sin(m\theta) \\ \sin(m\theta) & \cos(m\theta) \end{bmatrix}}_{\mathrm{R(m\theta)}} \begin{bmatrix} \mathrm{q_0} \\ \mathrm{q_1} \end{bmatrix}.\notag \end{align}\]For higher dimensions, (Su et al., 2021) proposes the 2-by-2 block-wise rotation matrix
\[\begin{equation} \mathrm{R_m} = \begin{bmatrix} \mathrm{\cos(m\theta_0)} & -\mathrm{\sin(m\theta_0)} & 0 & 0 & \cdots \\ \mathrm{\sin(m\theta_0)} & \;\cos(m\theta_0) & 0 & 0 & \cdots \\ 0 & 0 & \mathrm{\cos(m\theta_1)} & \mathrm{-\sin(m\theta_1)} & \cdots \\ 0 & 0 & \mathrm{\sin(m\theta_1)} & \;\cos(m\theta_1) & \cdots \\ \vdots & \vdots & \vdots & \vdots & \ddots \\ \end{bmatrix} \begin{bmatrix} \mathrm{q_0} \\ \mathrm{q_1} \\ \mathrm{q_2} \\ \mathrm{q_3} \\ \vdots \end{bmatrix}. \notag \end{equation}\]No Position Embeddings (NoPE)
RoPE is the mainstream choice for positional encoding, yet its performance decays rapidly as context length grows. NOPE (Kazemnejad et al., 2023) does not rely on any explicit positional encoding and offers a compelling way for length generalization. A hybrid strategy that alternates between RoPE and NoPE is also studied in SmolLM3.
The Transformer Family
Bidirectional Encoder Representations from Transformer (BERT)
BERT (Devlin et al., 2019) encodes bidirectional representations via masked language modeling. During pretraining, 15% of tokens are randomly selected; 80% are replaced with [MASK], 10% with a random token, and 10% left unchanged. Despite the bidirectional context, MLM breaks left-to-right (L2R) factorization, which makes exact sequence likelihood intractable and overlooks the higher-order dependencies. It is also harder to learn bidirectional representations.
To solve the undertrained issue, Robustly optimized BERT (RoBERTa) (Liu et al., 2019) trains the model with larger batches, more data, longer sequences, and the mask is also updated dynamically; ALBERT (Lan et al., 2019) is a light-weighted BERT that adopted factorized embedding and shared parameters across layers; DeBERTa (He et al., 2021) improves the performance via disentangled attention mechanism and enhanced mask decoders.
Generative Pre-trained Transformer (GPT)
GPT (Radford et al., 2018) trains a unidirectional, causally masked Transformer decoder to learn language representations. Its L2R factorization is compute-friendly and scales smoothly with model size, data, and compute, aligning with empirical scaling-law behavior. However, because self-attention is causal, each token can attend only to preceding context. This L2R constraint introduces several limitations, e.g. high latency for long sequences and limited parallelism at inference; exposure-bias error compounding; awkward infilling/ (mid-span) editing.
GPT-2 (1.5B) (Radford et al., 2019) is 10× larger than GPT and trained on millions of WebText tokens. It can be directly applied to downstream language tasks without parameter or architecture modifications (zero-shot transfer), demonstrating log-linear improvements in performance; GPT-3 (175B) (Brown et al., 2020) has the same architecture as GPT-2, except that the attention patterns are alternated between dense and sparse. GPT-3 shows impressive few-shot performance to many NLP tasks without any gradient-based fine-tuning.
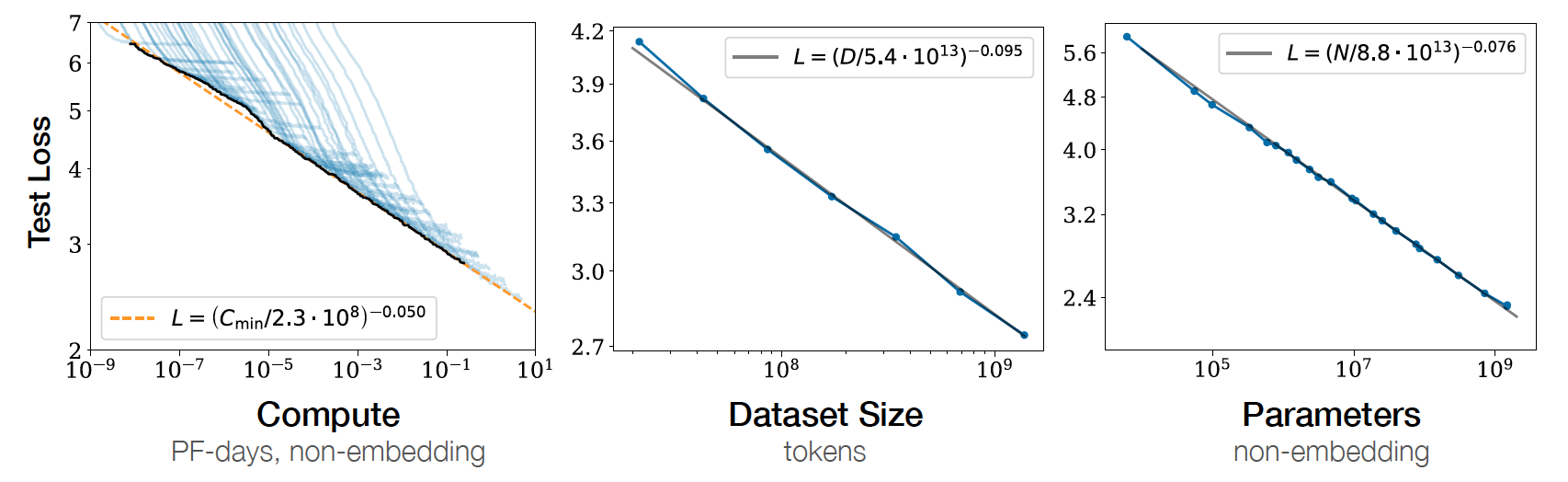
Scaling Laws
The test loss of a transformer yields a power-law with model size, dataset size, and computations (Kaplan et al., 2020). These scaling laws provide concrete guidance for allocating a fixed budget.
Citation
@misc{deng2025_inside_transformers,
title ={{Inside the Transformers}},
author ={Wei Deng},
journal ={waynedw.github.io},
year ={2025},
howpublished = {\url{https://www.weideng.org/posts/inside_transformers/}}
}
- Vaswani, A., S., N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., Kaiser, L., & Polosukhin, I. (2017). Attention Is All You Need. NIPS.
- Devlin, J., Chang, M.-W., Lee, K., & Toutanova, K. (2019). BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. NAACL-HLT.
- Bhojanapalli, S., Yun, C., Rawat, A. S., Reddi, S., & Kumar, S. (2020). Low-Rank Bottleneck in Multi-head Attention Models. ICML.
- Authors, D. S. (2024). DeepSeek-V2: A Strong, Economical, and Efficient Mixture-of-Experts Language Model. DeepSeek.
- Allal, L. B., Tunstall, L., Tazi, N., Bakouch, E., Beeching, E., Patiño, C. M., Fourrier, C., Frere, T., Lozhkov, A., Raffel, C., von Werra, L., & Wolf, T. (2025). The Smol Training Playbook: The Secrets to Building World-Class LLMs. Hugging Face.
- Katharopoulos, A., Vyas, A., Pappas, N., & Fleuret, F. (2020). Transformers are RNNs: Fast Autoregressive Transformers with Linear Attention. ICML.
- Jiang, A. Q., & Team, M. A. I. (2023). Mistral 7B. ArXiv Preprint ArXiv:2310.06825.
- Child, R., Gray, S., Radford, A., & Sutskever, I. (2019). Generating Long Sequences with Sparse Transformers. ArXiv Preprint ArXiv:1904.10509.
- Beltagy, I., Peters, M. E., & Cohan, A. (2020). Longformer: The Long-Document Transformer. ArXiv:2004.05150.
- Wang, S., Li, B. Z., Khabsa, M., Fang, H., & Ma, H. (2020). Linformer: Self-Attention with Linear Complexity.
- Choromanski, K., Likhosherstov, V., Dohan, D., Song, X., Gane, A., Sarlos, T., Hawkins, P., Davis, J., Mohiuddin, A., Kaiser, L., Belanger, D., Colwell, L., & Weller, A. (2021). Rethinking Attention with Performers. ICLR.
- Tay, Y., Dehghani, M., Bahri, D., & Metzler, D. (2022). Efficient Transformers: A Survey. ACM Computing Surveys (CSUR).
- Wang, K. A., Shi, J., & Fox, E. B. (2025). Test-time regression: a unifying framework for designing sequence models with associative memory.
- Yang, S., Wang, B., Shen, Y., Panda, R., & Kim, Y. (2024). Gated Linear Attention Transformers with Hardware-Efficient Training. ICML.
- Kitaev, N., Kaiser, L., & Levskaya, A. (2020). Reformer: The Efficient Transformer. International Conference on Learning Representations. https://openreview.net/forum?id=rkgNKkHtvB
- Rahimi, A., & Recht, B. (2007). Random Features for Large-Scale Kernel Machines. NIPS.
- Shaw, P., Uszkoreit, J., & Vaswani, A. (2018). Self-Attention with Relative Position Representations. NAACL HLT.
- Dai, Z., Yang, Z., Yang, Y., Carbonell, J., Le, Q. V., & Salakhutdinov, R. (2019). Transformer-XL: Attentive Language Models Beyond a Fixed-Length Context. ACL.
- Press, O., Smith, N. A., & Lewis, M. (2022). Train Short, Test Long: Attention with Linear Biases Enables Input Length Extrapolation. ICLR.
- Su, J., Lu, Y., Pan, S., Wen, B., & Liu, Y. (2021). RoFormer: Enhanced Transformer with Rotary Position Embedding. ArXiv Preprint ArXiv:2104.09864.
- Kazemnejad, A., Padhi, I., Natesan Ramamurthy, K., Das, P., & Reddy, S. (2023). The Impact of Positional Encoding on Length Generalization in Transformers. NeurIPS.
- Liu, Y., Ott, M., Goyal, N., Du, J., Joshi, M., Chen, D., Levy, O., Lewis, M., Zettlemoyer, L., & Stoyanov, V. (2019). RoBERTa: A Robustly Optimized BERT Pretraining Approach. ArXiv Preprint ArXiv:1907.11692.
- Lan, Z., Chen, M., Goodman, S., Gimpel, K., Sharma, P., & Soricut, R. (2019). ALBERT: A Lite BERT for Self-supervised Learning of Language Representations. ArXiv Preprint ArXiv:1909.11942. https://arxiv.org/abs/1909.11942
- He, P., Liu, X., Gao, J., & Chen, W. (2021). DeBERTa: Decoding-enhanced BERT with Disentangled Attention. International Conference on Learning Representations (ICLR).
- Raffel, C., Shazeer, N., Roberts, A., Lee, K., Narang, S., Matena, M., Zhou, Y., Li, W., & Liu, P. J. (2020). Exploring the Limits of Transfer Learning with a Unified Text-to-Text Transformer. Journal of Machine Learning Research, 21(140), 1–67.
- Radford, A., Narasimhan, K., Salimans, T., & Sutskever, I. (2018). Improving Language Understanding with Unsupervised Learning. OpenAI.
- Radford, A., Wu, J., Child, R., Luan, D., Amodei, D., & Sutskever, I. (2019). Language Models are Unsupervised Multitask Learners. OpenAI.
- Brown, T. B., Mann, B., Ryder, N., Subbiah, M., Kaplan, J., Dhariwal, P., Neelakantan, A., Shyam, P., Sastry, G., Askell, A., Agarwal, S., Herbert-Voss, A., Krueger, G., Henighan, T., Child, R., Ramesh, A., Ziegler, D. M., Wu, J., Winter, C., … Amodei, D. (2020). Language Models are Few-Shot Learners. ArXiv Preprint ArXiv:2005.14165.
- Kaplan, J., McCandlish, S., Henighan, T., Brown, T. B., Chess, B., Child, R., Gray, S., Radford, A., Wu, J., & Amodei, D. (2020). Scaling Laws for Neural Language Models. ArXiv Preprint ArXiv:2001.08361.