Mixture of Experts: Essentials
A sparse routing for scalable Transformers
Mixture of experts (MoE) scales model parameters and improves generation quality without increasing per-token FLOPs. Despite the name, MoE doesn’t mean assembling human-like experts (e.g., finance or medicine). Instead, it replaces a big feedforward network (FFN) (Shazeer et al., 2017) (Fedus et al., 2022) (Team, 2024) (OpenAI, 2025) with many smaller blocks, where only a subset is activated for each token.
This sparsity significantly increases model capacity while keeping computation efficient. It enables faster and more scalable training, improves utilization of available FLOPs, and supports efficient parallelism by distributing experts across different devices.
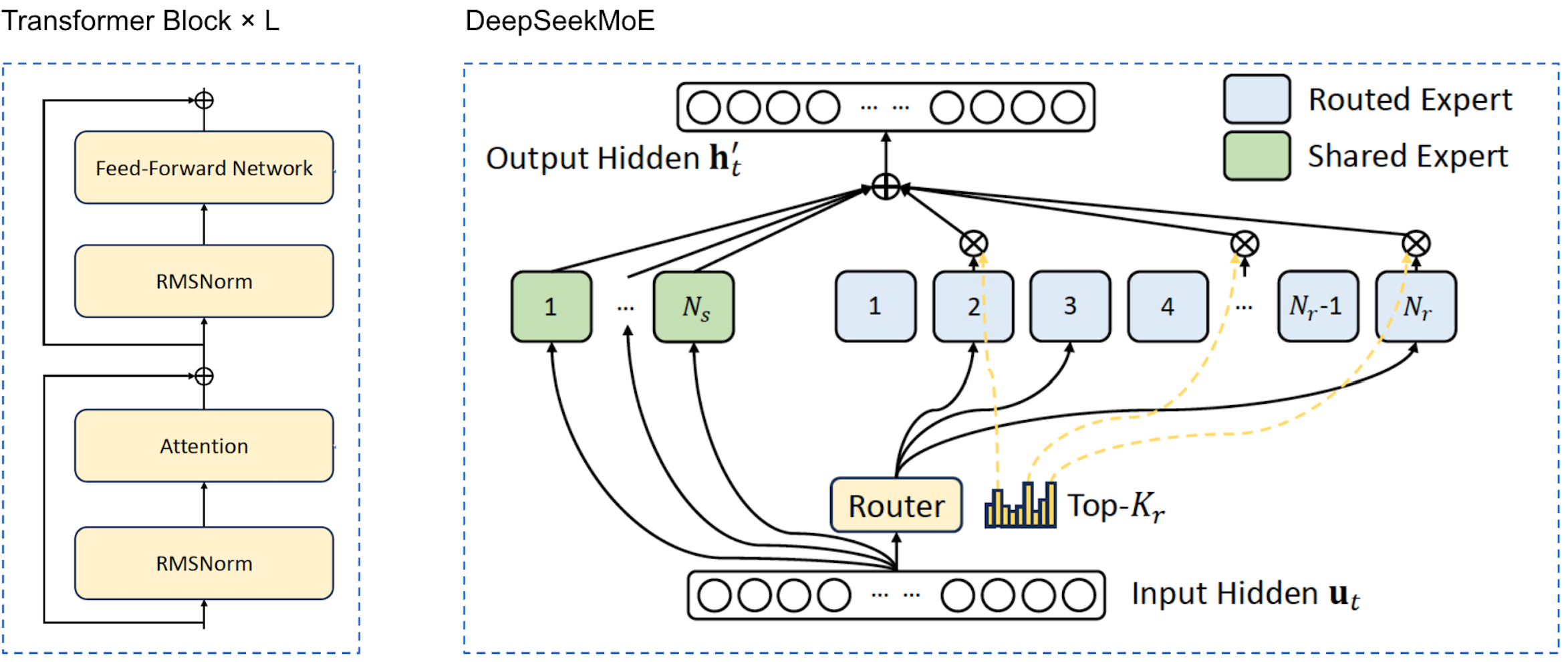
Routing
DeepSeekMoE introduces a hybrid design that combines shared experts with a gated mixture of routed experts:
\[\begin{align} \mathbf{h}'_t &= \mathbf{u}_t + \sum_{i=1}^{N_s} \mathrm{FFN}^{(s)}_i(\mathbf{u}_t) + \sum_{i=1}^{N_r} g_{i,t}\,\mathrm{FFN}^{(r)}_i(\mathbf{u}_t), \notag \\[6pt] g_{i,t} &= \mathrm{Softmax}\!\left(\mathbf{u}_t^{\top} \mathbf{e}_i \mathrm{ \ with\ topK \ masking} \right), \notag \\ % s_{i,t} % &= \mathrm{Sigmoid}\!\left(\mathbf{u}_t^{\top} \mathbf{e}_i\right). \notag \end{align}\]where $\mathbf{u_t}$ is the post-attention hidden state of the $t$-th token.
Similarly, GPT-OSS (OpenAI, 2025) adopts a closely related routing mechanism:
\[\begin{align} g_{i,t} &= \mathrm{Softmax}\!\left(z_{i,t} \mathrm{ \ with\ topK \ masking} \right) \notag \\ z_{i,t} &= \mathbf{w}_i^{\top}\,\mathrm{RMSNorm}(\mathbf{x}_t) + b_i. \notag \\ \end{align}\]MoE in GPT-OSS
In GPT-OSS, the MoE module is embedded directly inside the MLP block of each Transformer layer:
class TransformerBlock(torch.nn.Module):
def __init__(self, ...):
super().__init__()
self.layer_idx = layer_idx
self.attn = AttentionBlock(config, layer_idx, device)
self.mlp = MLPBlock(config, device)
def forward(self, x):
x = self.attn(x)
x = self.mlp(x)
return x
# Pre-normalization (RMSNorm)
# Note: normalization adds <0.2% FLOPs but can reduce runtime by >20%;
# bias is omitted for improved stability, consistent with modern Transformers.
class RMSNorm(nn.Module):
def __init__(self, hidden_size, eps=1e-6):
super().__init__()
self.eps = eps
self.weight = nn.Parameter(torch.ones(hidden_size))
def forward(self, x: torch.Tensor) -> torch.Tensor:
# Root Mean Square normalization
rms = x.pow(2).mean(dim=-1, keepdim=True)
x = x * torch.rsqrt(rms + self.eps)
return self.weight * x
Below is a simplified version of GPT-OSS MoE in the MLPBlock, focusing on core routing and expert computations:
class MLPBlock(nn.Module):
def __init__(self, hidden_size, intermediate_size, num_experts, experts_per_token, swiglu_limit):
super().__init__()
self.num_experts = num_experts
self.experts_per_token = experts_per_token
self.swiglu_limit = swiglu_limit
self.norm = RMSNorm(hidden_size)
self.gate = nn.Linear(hidden_size, num_experts)
# Expert parameters (maybe loaded from checkpoint)
self.mlp1_weight = nn.Parameter(torch.empty(num_experts, 2 * intermediate_size, hidden_size))
self.mlp1_bias = nn.Parameter(torch.empty(num_experts, 2 * intermediate_size))
self.mlp2_weight = nn.Parameter(torch.empty(num_experts, hidden_size, intermediate_size))
self.mlp2_bias = nn.Parameter(torch.empty(num_experts, hidden_size))
def forward(self, x: torch.Tensor) -> torch.Tensor:
u = self.norm(x)
logits = self.gate(u)
topk = torch.topk(logits, k=self.experts_per_token, dim=-1, sorted=True)
expert_idx = topk.indices
expert_w = F.softmax(topk.values, dim=-1)
W1 = self.mlp1_weight[expert_idx] # [B, K, 2M, H]
b1 = self.mlp1_bias[expert_idx] # [B, K, 2M]
h = torch.einsum("bekh,bh->bek", W1, u) + b1 # [B, K, 2M]
h = swiglu(h, limit=self.swiglu_limit) # [B, K, M]
W2 = self.mlp2_weight[expert_idx] # [B, K, H, M]
b2 = self.mlp2_bias[expert_idx] # [B, K, H]
y = torch.einsum("bekhm,bekm->bekh", W2, h) + b2 # [B, K, H]
out = torch.einsum("bekh,bek->bh", y, expert_w) # [B, H]
return x + out
Routing with REINFORCE
The routing decision in MoE models can be formulated as a reinforcement learning (RL) problem, where the router acts as a policy that selects a subset of experts for each token based on its hidden representation, and downstream task performance provides the reward signal (Clark et al., 2022). While policy-gradient methods such as REINFORCE offer a principled formulation, they suffer from high variance, slow convergence, and poor scalability in large language models.
Alternative approaches include formulating routing as an optimal transport problem to achieve balanced expert assignment, or introducing stochastic perturbations (Shazeer et al., 2017) to the gating mechanism to improve load balance and training stability.
Load Balancing
A key challenge in MoE models is the load imbalance, where a few experts receive most tokens. To avoid mitigate this issue, a differentiable load-balancing loss is commonly added to encourage uniform utilization and stable training (Fedus et al., 2022).
\[\mathrm{\mathcal{L}_{\text{lb}} = \alpha K \sum_{k=1}^K \langle f_k, P_j \rangle,}\]where $\mathrm{f_k=\mathrm{Avg}(\mathbb{1}(\text{Argmax}(p(x))=k))}$ is the fraction of tokens routed to expert $k$ and $\mathrm{P_j=\mathrm{Avg}(p_k(x))}$ is the average fraction for expert $k$ in a batch.
Fine-Tuning
During RL fine-tuning, MoE models can exhibit poor generalization due to over-specialized routing, policy collapse, or distribution shift amplified by sparse activation. Preventing overfitting in this regime remains an open problem. In practice, effective strategies include using more diverse fine-tuning data, constraining routing dynamics, and maintaining shared expert capacity.
Citation
@misc{deng2025MoE,
title ={{Mixture of Experts: Essentials}},
author ={Wei Deng},
journal ={waynedw.github.io},
year ={2025},
howpublished = {\url{https://weideng.org/posts/moe}}
}
- Shazeer, N., Mirhoseini, A., Maziarz, K., Davis, A., Le, Q., Hinton, G., & Dean, J. (2017). Outrageously Large Neural Networks: The Sparsely-Gated Mixture-of-Experts Layer. International Conference on Learning Representations (ICLR).
- Fedus, W., Zoph, B., & Shazeer, N. (2022). Switch Transformers: Scaling to Trillion Parameter Models with Simple and Efficient Sparsity. Journal of Machine Learning Research, 23(120), 1–39. https://jmlr.org/papers/v23/21-0998.html
- Team, D. S.-A. I. (2024). DeepSeek-V3 Technical Report. arXiv preprint arXiv:2412.19437. https://arxiv.org/abs/2412.19437
- OpenAI. (2025). openai/gpt-oss: Open-Weight GPT-OSS Models. https://github.com/openai/gpt-oss
- Clark, A., de las Casas, D., Guy, A., Mensch, A., Paganini, M., Hoffmann, J., Damoc, B., Hechtman, B., Cai, T., Borgeaud, S., van den Driessche, G., Rutherford, E., Hennigan, T., Johnson, M., Millican, K., Cassirer, A., Jones, C., Buchatskaya, E., Budden, D., … Simonyan, K. (2022). Unified Scaling Laws for Routed Language Models. ICML.