Replica Exchange and Variance Reduction

Variance-reduced sampling algorithms (Dubey et al., 2016) (Xu et al., 2018) are not widely adopted in practice. Alternatively, we focus on the energy variance reduction to exploit exponential accelerations but no longer consider the gradient variance reduction.

To this end, we consider a standard sampling algorithm, the stochastic gradient Langevin dynamics (SGLD), which is a mini-batch numerical discretization of a stochastic differential equation (SDE) as follows:

$${\beta }_{\mathrm{k}+1}={\beta }_{\mathrm{k}}-\eta \frac{\mathrm{N}}{\mathrm{n}}\mathrm{\nabla }\sum _{\mathrm{i}\in \mathrm{B}}\mathrm{L}({\mathrm{x}}_{\mathrm{i}}|{\beta }_{\mathrm{k}})+\sqrt{2\eta {\tau }_1}{\xi }_{\mathrm{k}},$$

where $\beta \in {\mathbb{R}}^{\mathrm{d}}$, $\mathrm{L}({\mathrm{x}}_{\mathrm{i}}|\beta )$ is the energy function based on the i-th data point and B denotes a data set of size $n$ simulated from the whole data of size $\mathrm{N}$. $\xi$ is a d-dimensional Gaussian vector. It is known that a non-convex $\mathrm{U}(\cdot )$ often leads to an exponentially slow mixing rate.

To accelerate the simulations, replica exchange proposes to run multiple stochastic processes with different temperatures, where interactions between different SGLD chains are conducted in a manner that encourages large jumps (Yin & Zhu, 2010) (Chen et al., 2019) (Deng et al., 2020) (Deng et al., 2021).

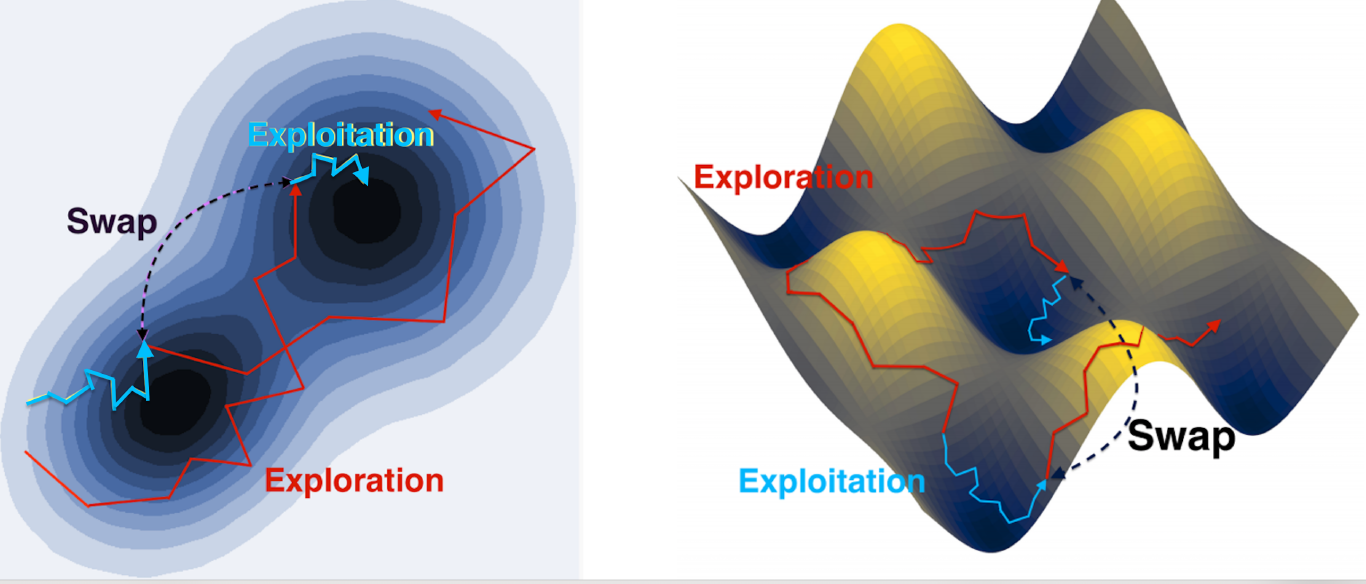
In particular, the parameters swap the positions with a probability $1\wedge S({\beta }^{(1)},{\beta }^{(2)})$

$$\mathrm{S}({\beta }^{(1)},{\beta }^{(2)})={\mathrm{e}}^{(\frac{1}{{\tau }_1}-\frac{1}{{\tau }_2})(\frac{\mathrm{N}}{\mathrm{n}}\sum _{\mathrm{i}\in \mathrm{B}}\mathrm{L}({\mathrm{x}}_{\mathrm{i}}|{\beta }^{(1)})-\frac{\mathrm{N}}{\mathrm{n}}\sum _{\mathrm{i}\in \mathrm{B}}\mathrm{L}({\mathrm{x}}_{\mathrm{i}}|{\beta }^{(2)})-(\frac{1}{{\tau }_1}-\frac{1}{{\tau }_2}){\sigma }^2)},$$

where ${\sigma }^2$ is the variance of the noisy estimators $\sum _{\mathrm{i}\in \mathrm{B}}\mathrm{L}({\mathrm{x}}_{\mathrm{i}}|\cdot )$. Under Normality assumptions, the above rule leads to an unbiased swapping probability, which satisfy the detailed balance in a stochastic sense. However, the efficiency of the swaps are significantly reduced due to the requirement of corrections to avoid biases.

The desire to obtain more effective swaps drives us to design more efficient energy estimators. To reduce the variance of the noisy energy estimator $\mathrm{L}(\mathrm{B}|{\beta }^{(\mathrm{h})})=\frac{\mathrm{N}}{\mathrm{n}}\sum _{\mathrm{i}\in \mathrm{B}}\mathrm{L}({\mathrm{x}}_{\mathrm{i}}|{\beta }^{(\mathrm{h})})$ for $\mathrm{h}\in 1,2$, we consider an unbiased estimator $\mathrm{L}(\mathrm{B}|{\hat{\beta }}^{(\mathrm{h})})$ for $\sum _{\mathrm{i}=1}^{\mathrm{N}}\mathrm{L}({\mathrm{x}}_{\mathrm{i}}|{\hat{\beta }}^{(\mathrm{h})})$ and a constant $c$, we see that a new estimator $\tilde{\mathrm{L}}(\mathrm{B}|{\beta }^{(\mathrm{h})})$, which follows $$\tilde{\mathrm{L}}(\mathrm{B}|{\beta }^{(\mathrm{h})})=\mathrm{L}(\mathrm{B}|{\beta }^{(\mathrm{h})})+\mathrm{c}(\mathrm{L}(\mathrm{B}|{\hat{\beta }}^{(\mathrm{h})})-\sum _{\mathrm{i}=1}^{\mathrm{N}}\mathrm{L}({\mathrm{x}}_{\mathrm{i}}|{\hat{\beta }}^{(\mathrm{h})})),$$ is still the unbiased estimator for $\sum _{\mathrm{i}=1}^{\mathrm{N}}\mathrm{L}({\mathrm{x}}_{\mathrm{i}}|{\beta }^{(\mathrm{h})})$. Moreover, energy variance reduction potentially increases the swapping efficiency exponentially given a larger batch size $n$, a small learning rate $\eta$, and a more frequent update of control variate $\hat{\beta }$, i.e. a small $m$

$$\mathrm{Var}(\tilde{\mathrm{L}}(\mathrm{B}|{\beta }^{(\mathrm{h})}))\le \mathrm{O}\left(\frac{{\mathrm{m}}^2\eta }{\mathrm{n}}\right).$$

The following shows a demo that explains how variance-reduced reSGLD works.