Sequence GAN Explained
Adversarial generations of discrete sequences
Generative Adversarial Networks (GANs) (Goodfellow et al., 2014) were once among the best generative models for image data. Their adversarial training enables the generator (\(\mathbf{G_{\theta}}\)) to produce high-fidelity samples that even a strong discriminator (\(\mathbf{D_{\phi}}\)) cannot distinguish. \(\mathbf{D_{\phi}}\) and \(\mathbf{G_{\theta}}\) play the minimax game:
\[\begin{align} & \mathrm{\min_{G_{\theta}} \max_{D_{\phi}} \mathbb{E}_{x \sim p_{\text{data}}(x)} [\log D_{\phi}(x)] + \mathbb{E}_{z\sim G_{\theta}} [\log(1 - D_{\phi}(z))]}. \notag \end{align}\]Despite this success, however, its generation of discrete sequences remains poorly understood due to:
- The loss of \(\mathbf{D_{\phi}}\) from \(\mathbf{G_{\theta}}\) samples is not non-differentiable on discrete data;
- \(\mathbf{D_{\phi}}\) cannot evaluate an intermediate state \(\mathrm{z_{1:t}}\) unless \(\mathrm{t}\) reaches the full sequence length \(\mathrm{T}\).
Sequence Generative Adversarial Nets (SeqGAN)
SeqGAN resolves these issues by modeling the generator \(\mathbf{G_{\theta}}\) as a policy model for sequence generation and using the discriminator \(\mathbf{D_{\phi}}\) to provide the reward signal.
Intermediate state \(\mathrm{z_{1:t}}\): SeqGAN performs Monte Carlo rollouts using the policy model \(\mathrm{G_{\theta}}\) to sample the remaining steps such as
\[\begin{align} & \mathrm{\{z_{1:T}^n\}_{n=1}^N \sim \text{Rollout}^{G_{\theta}}(z_{1:t}), \text{where}\ \ z_{1:t}^n=z_{1:t}}. \notag \end{align}\]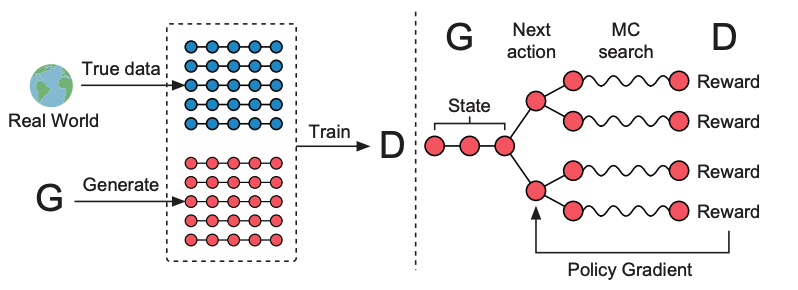
Non-differentiability: Policy gradient methods (Williams, 1992) are proposed to train \(\mathbf{G_{\theta}}\) by shifting from the gradient of discrete actions to the probability space using the log-derivative trick:
\[\begin{align} & \nabla_{\theta} \mathrm{\mathbb{E}_{z_{t}\sim G_{\theta}(\cdot\mid z_{1:t-1})}[D_{\phi}^t(z_{1:t})]=\mathbb{E}_{z_{t}\sim G_{\theta}(\cdot\mid z_{1:t-1})}[D_{\phi}^t(z_{1:t}) \nabla_{\theta} \log G_{\theta}(z_t\mid z_{1:t-1})]}, \label{pg} \end{align}\]where \(\mathrm{D_{\phi}^t}\) is the intermediate reward signal estimated from Monte Carlo rollout samples:
\[\begin{align} & \mathrm{D^t_{\phi}(z_{1:t})} = \begin{cases} \displaystyle \mathrm{\frac{1}{N} \sum_{n=1}^N D_{\phi}(z_{1:T}^n), \quad z^{n}_{1:T} \sim \mathrm{Rollout}^{G_\theta}(z_{1:t})}, & \mathrm{t < T} \\[10pt] \mathrm{D_\phi(z_{1:t})}, & \mathrm{t = T.} \end{cases} \notag \end{align}\]The optimization of \(\mathbf{G_{\theta}}\) is equivalent to maximizing the reward using policy gradients, as implied by \eqref{pg}:
\[\begin{align} & \mathrm{R(\theta)=\sum_{t=1}^T \mathbb{E}_{z_{t}\sim G_{\theta}(\cdot\mid z_{1:t-1})}[D_{\phi}^t(z_{1:t})] \iff \nabla_{\theta} R(\theta)=\sum_{t=1}^T \mathbb{E}_{z_{t}\sim G_{\theta}(\cdot\mid z_{1:t-1})}[D_{\phi}^t(z_{1:t})\nabla_{\theta} \log G_{\theta}(z_t\mid z_{1:t-1})]}. \notag \end{align}\]Applications in On-Policy Distillation
The above framework finds perfect applications in on-policy distillation (Ye et al., 2025) (Zheng et al., 2025) to enabling the distillation of domain-expert models or ultra-fast generators.
The generator (policy model) can be the student LLM (fine-tuned Qwen) or dLLM; the discriminator(reward model) is the tweaked generator model with an extra prediction head; GPT or LLaDA can be the teacher model. The policy learning can be further enhanced by GRPO (Shao et al., 2024) to reduce the variance.
Applications in Adversarial Preference Optimization (APO)
Adversarial Preference Optimization (APO) (Cheng et al., 2024) introduces a SeqGAN-style or SAIL (Ho & Ermon, 2016) adversarial loop into modern LLM alignment. Instead of using a fixed reward model (RM), APO lets the policy (LLM) and reward model co-evolve: the LLM generates high-reward responses while the RM discriminates between golden data and model samples.
APO formulates a Wasserstein GAN-like minimax objective:
\[\begin{align} \mathrm{\min_{r_\phi}\max_{\pi_\theta}\ \mathbb{E}_{y\sim\pi_\theta} \big[ r_\phi(x,y) \big] - \mathbb{E}_{y\sim P_{\text{gold}}} \big[ r_\phi(x,y) \big].} \end{align}\]Training alternates between updating the RM with real vs. model responses and updating the LLM with offline preference-optimization methods (DPO, RRHF, GRPO), requiring no extra human labels. Conceptually, APO is a preference-driven analog of SeqGAN/ SAIL, leveraging adversarial learning to align sequence models.
Citation
@misc{deng2025seqGAN,
title ={{Sequence GAN Explained}},
author ={Wei Deng},
journal ={waynedw.github.io},
year ={2025},
howpublished = {\url{https://weideng.org/posts/seqGAN}}
}
- Goodfellow, I. J., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., Courville, A., & Bengio, Y. (2014). Generative Adversarial Networks. Advances in Neural Information Processing Systems, 27.
- Yu, L., Zhang, W., Wang, J., & Yu, Y. (2017). SeqGAN: Sequence Generative Adversarial Nets with Policy Gradient. AAAI Conference on Artificial Intelligence (AAAI).
- Williams, R. J. (1992). Simple statistical gradient-following algorithms for connectionist reinforcement learning. Machine Learning, 8(3–4), 229–256.
- Ye, T., Dong, L., Chi, Z., Wu, X., Huang, S., & Wei, F. (2025). Black-Box On-Policy Distillation of Large Language Models. ArXiv Preprint ArXiv:2511.10643.
- Zheng, H., Liu, X., Kong, C. X., Jiang, N., Hu, Z., Luo, W., Deng, W., & Lin, G. (2025). Ultra-Fast Language Generation via Discrete Diffusion Divergence Instruct. ArXiv Preprint ArXiv:2509.25035.
- Shao, Z., Wang, P., Zhu, Q., Xu, R., Song, J., Bi, X., Zhang, H., Zhang, M., Li, Y. K., Wu, Y., & others. (2024). DeepseekMath: Pushing the Limits of Mathematical Reasoning in Open Language Models. ArXiv Preprint ArXiv:2402.03300.
- Cheng, P., Yang, Y., Li, J., Dai, Y., Hu, T., Cao, P., Du, N., & Li, X. (2024). Adversarial Preference Optimization: Enhancing Your Alignment via RM-LLM Game. Findings of the Association for Computational Linguistics: ACL 2024.
- Ho, J., & Ermon, S. (2016). Generative Adversarial Imitation Learning. Advances in Neural Information Processing Systems (NeurIPS), 4565–4573.